Periodic functions are functions that repeat its values over and over, after some definite period or cycle on a specific period. This can be expressed mathematically that A function f is said to be periodic if there exists a real T>0 such that f (x+T) = f(x) for all x.

The fundamental period of a function is the length of a smallest continuous portion of the domain over which the function completes a cycle. That is, it's the smallest length of domain that if you took the function over that length and made an infinite number of copies of it, and laid them end to end, you would have the original function.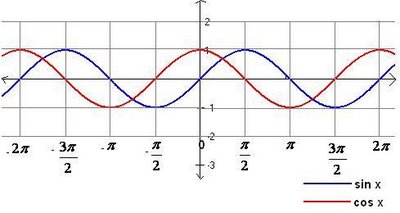



If a function is periodic, then the smallest t>0 ,if it exists such that f (x+t) = f(x) for all x, is called the fundamental period of the function.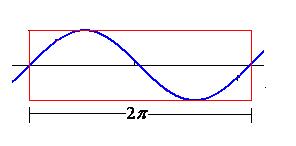


The trigonometric functions sine and cosine are common periodic functions, with period 2π.
ie. sin (x+2π)= sin x , cos(x+2π)=cos x

But tan and cot remain unchanged when x is increased by pi.
ie. tan(x+π)=tan x, cot(x+π)= cot x
So, they are periodic functions with period π .

An aperiodic function (non-periodic function) is one that has no such period